cleaningsraka.blogg.se - Peg solitaire solving algorithm

#Peg solitaire solving algorithm cracker
#Peg solitaire solving algorithm code

I know Python uses pass by reference so I was a bit unsure as to whether I'd be able to use a recursion tree effectively so this is why I used deep copy, so that there is a previous version of the board and temp_stack to revert to when the back tracking occurs. The idea is that when the game ends, the program backs out of the recursion tree and picks up where it left off in the main loop. Recursion happens as move is called again with the copies as arguments. If a move can be made, it deep copies a new board and stack (so there can be fresh, new objects being passed into the recursion tree), adjusts the board copy, and updates the temp_stack copy that a new move has been made. If the game is not over, it cycles through the list of all possible moves and checks to see which ones that apply to the state of the board that has been passed through as a parameter. It appends to the simulation.moves list a snapshot of the game and returns. So, when move is called, it checks to see if there are any moves left. board.poss_moves is a list of all possible moves the 5 row triangle board contains.board is a board object and temp_stack is the running stack for a current try at solving the game.It also has as one of its members a list called moves, which stores all the moves for each possible path that can be taken for each game. There is a Simulation class that instantiates a simulation object, which contains the move() function.The background you may need to understand it is as follows:

#Peg solitaire solving algorithm code

Turns out C++ probably wouldn't have been too bad a choice but I'm enjoying the experience of learning Python.īelow, you'll find the code for the main recursive algorithm for moving along the board and solving it. Taking user-entered strings and using them as integers is just easier in interpreted languages.I initially thought my data structure would be more involved so I chose Python over C++ to open up the opportunity to use dictionaries.I'm new to Python so I want to learn it.I chose Python as my language of choice for a few reasons:

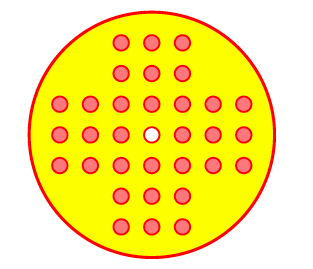
My solver will solve for all solutions for a given starting hole, whether the game ends with one peg, two, etc.

$peg solitaire solving algorithm$

It's the game where you start out with pegs in holes, with one hole empty, then jump pegs (like checkers) and try to get exactly one peg remaining in the end.

#Peg solitaire solving algorithm cracker

It will allow the user to select the shape of the board in the future but for now I'm testing it with a standard 5 row triangle game, like the ones you find in Cracker Barrel. I am in the process of writing a peg solitaire solver in Python.

We only need to check half of the board, as the solutions of the other half would be symmetrical.īut despite these the code is still very slow.Hello, all.

Optimizations I have come up with so far: If re.search(expression1, string) or re.search(expression2, string): If board and board and not board:Įxpression1 = '1000+1' #RE for a proven to be unsolvable boardĮxpression2 = '00100' #RE for a proven to be unsolvable board So I was wondering if there are some optimizations I could do or different solution approaches. I have created a brute force algorithm which finds all the possible moves until a valid solution is reached, but it starts taking a very long time to find a solution past n > 20. The goal of the algorithm I am trying to make is to take an input of n where n > 2 and n is an even number, then for a board of length n, find all the positions for a start state at which a hole can be placed to produce a valid solution. So for a board such as board = there are two available moves. Your available moves at any given position is to move one peg by two positions to the right or to the left if and only if there is a peg between the two position, then once you make that move, replace the middle peg with a hole. The goal of the game is to reach a board state where n-1 elements are holes and 1 element is a peg at any given position. So a starting position can be where 1s represent pegs and 0s represent holes for n = 6 n-1 elements are pegs (filled) and 1 element is a hole (empty). You initially start with a 1 dimensional board of length n. First I will explain the rules of peg solitaire (for 1 dimension):